集合の演算を行う(和集合、積集合、差集合、対称差集合)

集合と集合の演算を行い、和集合、積集合、差集合、対称差集合をそれぞれ求める方法について解説します。

(Last modified: 2024-09-16)

和集合を求める

和集合とは 2 つの集合の少なくともどちらか 1 つに含まれる要素の集合のことです。

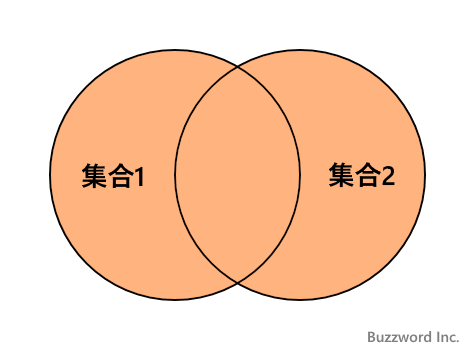
和集合を求めるには、演算子の | を使用するか、 set 型および frozenset 型で用意されている union メソッドを使用します。

集合 = 集合1 | 集合2
集合 = 集合1.union(集合2)

どちらも 集合1 と 集合2 の和集合として新しい集合を返します。

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

print(set1 | set2)
>> {'B', 'D', 'E', 'C', 'F', 'A'}
print(set1.union(set2))
>> {'B', 'D', 'E', 'C', 'F', 'A'}

3 つ以上の集合について和集合を求めることもできます。(この後で解説する積集合や差集合でも同様です)。

集合 = 集合1 | 集合2 | 集合3 | ...
集合 = 集合1.union(集合2, 集合3, ...)

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}
set3 = {"A", "C", "E", "G"}

print(set1 | set2 | set3)
>> {'G', 'B', 'D', 'E', 'C', 'F', 'A'}

和集合を新しい集合として取得するのではなく、最初の集合にそのまま保存するには。演算子の |= を使用するか set 型で用意されている update メソッドを使用します。

集合1 |= 集合2
集合1.update(集合2)

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

set1.update(set2)
print(set1)
>> {'B', 'D', 'E', 'C', 'F', 'A'}

積集合を求める

積集合とは 2 つの集合の両方に含まれる要素の集合のことです。

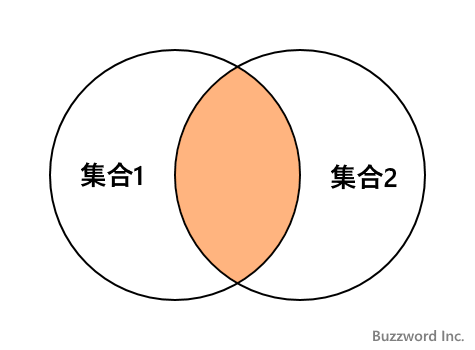
積集合を求めるには、演算子の & を使用するか、 set 型および frozenset 型で用意されている intersection メソッドを使用します。

集合 = 集合1 & 集合2
集合 = 集合1.intersection(集合2)

どちらも 集合1 と 集合2 の積集合として新しい集合を返します。

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

print(set1 & set2)
>> {'D', 'C'}
set1.intersection(set2)
>> {'D', 'C'}

積集合を新しい集合として取得するのではなく、最初の集合にそのまま保存するには。演算子の &= を使用するか set 型で用意されている intersection_update メソッドを使用します。

集合1 &= 集合2
集合1.intersection_update(集合2)

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

set1.intersection_update(set2)
print(set1)
>> {'D', 'C'}

差集合を求める

差集合とは集合 1 に含まれているけれど集合 2 には含まれていない要素の集合のことです。

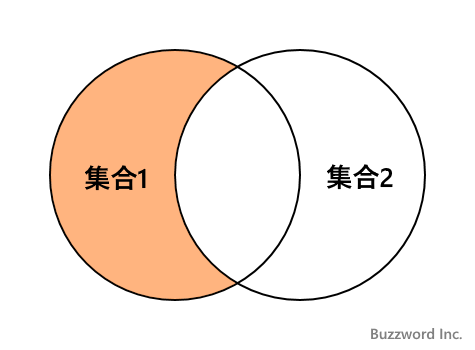
差集合を求めるには、演算子の - を使用するか、 set 型および frozenset 型で用意されている difference メソッドを使用します。

集合 = 集合1 - 集合2
集合 = 集合1.difference(集合2)

どちらも 集合1 と 集合2 の差集合として新しい集合を返します。

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

print(set1 - set2)
>> {'A', 'B'}
print(set1.difference(set2))
>> {'A', 'B'}

差集合を新しい集合として取得するのではなく、最初の集合にそのまま保存するには。演算子の -= を使用するか set 型で用意されている difference_update メソッドを使用します。

集合1 -= 集合2
集合1.difference_update(集合2)

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

set1 -= set2
print(set1)
>> {'B', 'A'}

対称差集合を求める

対称差集合とは 2 つの集合のどちらか片方だけに含まれる要素の集合のことです。

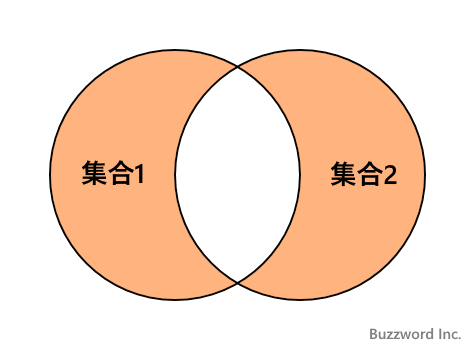
対称差集合を求めるには、演算子の ^ を使用するか、 set 型および frozenset 型で用意されている symmetric_difference メソッドを使用します。

集合 = 集合1 ^ 集合2
集合 = 集合1.symmetric_difference(集合2)

どちらも 集合1 と 集合2 の対称差集合として新しい集合を返します。

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

print(set1 ^ set2)
>> {'F', 'B', 'E', 'A'}
print(set1.symmetric_difference(set2))
>> {'F', 'B', 'E', 'A'}

積集合を新しい集合として取得するのではなく、最初の集合にそのまま保存するには。演算子の ^= を使用するか set 型で用意されている symmetric_difference_update メソッドを使用します。

集合1 ^= 集合2
集合1.symmetric_difference_update(集合2)

具体的には次のように記述します。

set1 = {"A", "B", "C", "D"}
set2 = {"C", "D", "E", "F"}

set1 ^= set2
print(set1)
>> {'B', 'E', 'F', 'A'}

-- --

集合と集合の演算を行い、和集合、積集合、差集合、対称差集合をそれぞれ求める方法について解説しました。

著者 / TATSUO IKURA

これから IT 関連の知識を学ばれる方を対象に、色々な言語でのプログラミング方法や関連する技術、開発環境構築などに関する解説サイトを運営しています。